Anexo

PLANTEAMIENTO 1

(Para resolverse de manera individual)

Tenemos dos tarros grandes. Uno de ellos está lleno de un gran número de bolitas azules; el otro, con igual número de bolitas rojas. De este último se sacan con un cucharón cinco bolitas rojas, que son depositadas y entremezcladas con las bolitas azules del otro. Después una persona mete la mano en el tarro de las bolitas azules y, sin mirar de qué color son, entresaca cinco bolitas, que deja caer en el tarro de las rojas. ¿Habrá finalmente en el tarro de las bolas rojas igual número de bolas de ese color que de azules en el tarro de las azules?

BRANSFORD, John D. y Barry S. STEIN, Solución ideal de problemas: guía para mejor pensar, aprender y crear, Barcelona, Labor, 1988. p. 35.

PLANTEAMIENTO 2

(Para resolverse en equipo)

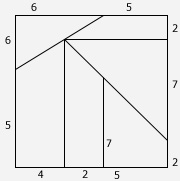
El dibujo que aparece abajo es un rompecabezas, se trata de que ustedes hagan uno semejante, pero más grande, de manera que la parte que mide 4, deberá medir 7 en el rompecabezas que ustedes harán. Primero pónganse de acuerdo en el procedimiento que van a usar y luego se reparten las piezas para que cada quien haga una o dos.

Si lo consideran necesario, utilicen hojas, reglas y tijeras.

SEP, La enseñanza de las matemáticas en la escuela primaria. Lecturas,
México, SEP, 1995. p. 178.

PLANTEAMIENTO 3

(Para resolverse de manera individual)

Lea cuidadosamente una sola vez el párrafo siguiente. Después responda las preguntas que se hacen a continuación.

Es usted el conductor de un autobús que puede llevar en total a 72 pasajeros (hay 36 asientos dobles). En la primera parada suben al autobús 7 personas.

En la parada siguiente, bajan 3 y suben 5. En la siguiente, bajan 4 personas y suben 2. En la posterior, bajan 5 pasajeros y suben 7. Cuando el autobús llega a su penúltima parada, suben 2 personas y 5 bajan.

¿Cuántas paradas hizo el autobús? ¿Cómo se llama el conductor del autobús? Al llegar a la terminal, ¿cuántas personas quedan en el autobús?

BRANSFORD, John D. y Barry S. STEIN, op. cit., Barcelona,
Labor, 1988. pp. 56, 163.

PLANTEAMIENTO 4

(Para resolverse de manera individual o en equipo)

Hay cinco cajas de refresco en un lugar y tienen que llevarse a diferentes sitios como sigue: la primera a 10 metros de distancia del origen, la segunda a 20 metros, la tercera a 30 metros y así sucesivamente hasta colocarlas siempre a 10 metros de la anterior. En cada movimiento la persona sale del origen, lleva la caja al lugar que corresponde y regresa al lugar de origen. Este proceso se repite hasta mover todas las cajas y regresar al punto de origen. Si sólo se puede llevar una caja en cada intento, ¿cuántos metros habrá recorrido la persona al finalizar la tarea?

SÁNCHEZ de, Margarita A., Desarrollo de habilidades del pensamiento,
Trillas, México, 1999. p. 457.